V4: Introduction to regularization in mixed models
What is this regularization and why don’t we analyze the data in 2 stages?
Introduction
This chapter is paired with the fourth video in the mixed model series, What is this regularization and why don’t we analyze the data in 2 stages?. Although the two-stage formulation is a great way to conceptualize the mixed model, it also might inspire a shortcut for data analysis: the two-stage summary statistics approach. For those familiar with fMRI data, this is exactly what is done to analyze those data due to the complexity and structure of the data. The approaches vary greatly across software packages where the SPM approach is most similar to what will be done here, but I will not be making comparisons with or between fMRI software. There is a related paper, written by myself and others that compares the models of different fMRI software packages.
There are many reasons why the all-in-one mixed model, which I will just call a mixed model or MM from now on, is better than using the two-stage summary statistics approach (called 2SSS from now on). For one, you are not allowed simplified or more complex random effects structures. For example, there may be cases where a within-subject variable will not be specified as random and you cannot really do this using 2SSS. There are other reasons that will come up as we work through this topic. The most compelling reason for the user might be that a mixed model takes about one line of code versus many lines of code for the summary statistics approach.
Regularization: key difference
What about when the 2SSS and MM formulations are quite close? How does the mixed model result differ? Sometimes they’ll be almost identical, but other times they will be quite different. Why? The short answer is the within-subject values related to the fixed effects are regularized in a mixed model and that is the focus here. This is a bit of a confusing statement because within-subject estimates are not actually estimated! Assume we are working with the sleepstudy data, which would include a within- and between-subject variability. Recall the mixed model equation, \[Y_i = X_i\beta + Z_ib_i + \epsilon_i,\] where \(Y_i\) is the dependent variable for subject \(i\), \(X_i\) is the design matrix for the fixed effects (see the last chapter for more details), \(\beta\) is the group parameter vector, \(Z_i\) is a matrix for the random effects, \(b_i\) are the random effects describing between-subject variability, and \(\epsilon_i\) is describes the within-subject variability. There are not any within-subject parameters estimated in this model. The term, \(b_i\) is a random variable that describes the between-subject distribution, \(b_i \sim N(0, G)\). Importantly, the \(b_i\) are not estimated, but the corresponding covariance of the \(b_i\), \(G\), is estimated and serves as the between-subject variability estimate. Although the subject specific estimates are not estimated, the subjects with less data will contribute less to the estimate of the group parameter, \(\beta\). Much, much more exploration will be done on this topic as time goes on.
For now I would like to illustrate what the regularization looks like for means, but there isn’t a perfect way to illustrate it. Typically the regularization is shown by comparing within-subject estimates to predicted within-subject estimates from the mixed model, based on values called BLUPS or best linear unbiased predictors. Some are not fans of this term, so I will simply refer to these as conditional modes, following the notation used by Douglas Bates, the author of the lme4 library. As stated in a draft of his book, “it is an appealing acronym, I don’t find the term particularly instructive (what is a ‘linear unbiased predictor’ and in what context are these the ‘best’?) and prefer the term conditional mode.” (book can be found here at the time of this writing). The reason why this isn’t the perfect way of illustrating regularization is because it doesn’t perfectly reflect how the regularization ends up impacting the group-level results. That will be the focus in the future, but now the goal is to understand that there is regularization happening.
The specific goal of the simulations below is to understand the impact of regularization by looking at estimates based on within-subject averages from the first stage of 2SSS and the conditional modes from mixed models. The first level estimates from 2SSS will be referred to as OLS (Ordinary Least Squares) estimates or \(\hat\beta_i^{OLS}\) and the conditional modes will be called just that or referred to as \(\hat\beta_i\).
What is a conditional mode?
In an effort to keep equations at a minimum, I will explain conditional model conceptually. For more information I recommend looking at the Bates book I linked to above or the textbook, “Applied Longitudinal Analysis” by Fitzmaurice, Laird and Ware. To understand the difficulty of this problem, remind yourself that typically when we have a random variable that follows a distribution, say \(X \sim N(\mu, \sigma^2)\), we focus on the estimation of \(\mu\) and \(\sigma^2\). Asking what value \(X\) is doesn’t even make much sense, since it is a a random variable. What can be done is to use the mode of the distribution as a prediction of \(X\), which is where the “mode” in “conditional mode” comes from. The conditioning part is somewhat simple. The mixed model equation above describes the distribution of \(Y_i\) but we want the distribution of \(b_i\) for a specific subject, \(i\). To get at this, the distribution of the random effects conditional on the data, \(Y\), is used. The part of this process that is very different from when we estimate things, is that estimated parameters (within-subject variance, between-subject covariance and fixed effects) are substituted in place of the truth in the distributions in order to derive these modes instead of the true values because they are unknown. This introduces an additional source of variability. The take-away is simply, again, the within-subject estimates are not estimated by default in a mixed model but we can predict them using conditional modes. These predictions can be quite noisy because they rely on estimates of parameters in order to specify the conditional distribution.
Next, some fake data will be generated and used to estimate some conditional modes and start building intuition about the regularization in mixed models. Fake data are used for the convenience of knowing the truth.
Simulated data
The simulated data consist of 10 subjects where 5 have 50 observations and 5 only have 5 observations from some type of behavioral experiment measuring reaction time. As in the last chapter, the two-stage random effects formulation will be used to simulate the data.
library(lme4)
library(lmerTest)
library(ggplot2)
# Simulate true subject-specific means:
nsub = 10
btwn.sub.sd = 10
#within-subject means
win.means = rnorm(nsub, mean = 250, sd = btwn.sub.sd)
# Simualte data for each subject by wiggling around their means
win.sub.sd = 20
# The following indicates how many data per subject, the first 5 only have 5 observations.
n.per.sub = rep(50, nsub)
n.per.sub[1:5] = 5
rt = c()
subid = c()
for (i in 1:nsub){
rt.loop = rnorm(n.per.sub[i], win.means[i], sd = win.sub.sd)
rt = c(rt, rt.loop)
subid = c(subid, rep(i, n.per.sub[i]))
}
dat = data.frame(subid, rt)Here is a plot of the resulting data. As you can see the first five subjects have much less data than the rest of the subjects. This was done on purpose to illustrate the regularization since the factor that impacts the regularization is the amount of data within-subject. There is much more to this, but it will be covered in the following chapters.
ggplot(dat, aes(x=as.factor(subid), y = rt)) +
geom_boxplot() +
geom_jitter(shape=16, position=position_jitter(0.2)) +
xlab("Subject")+ylab("RT")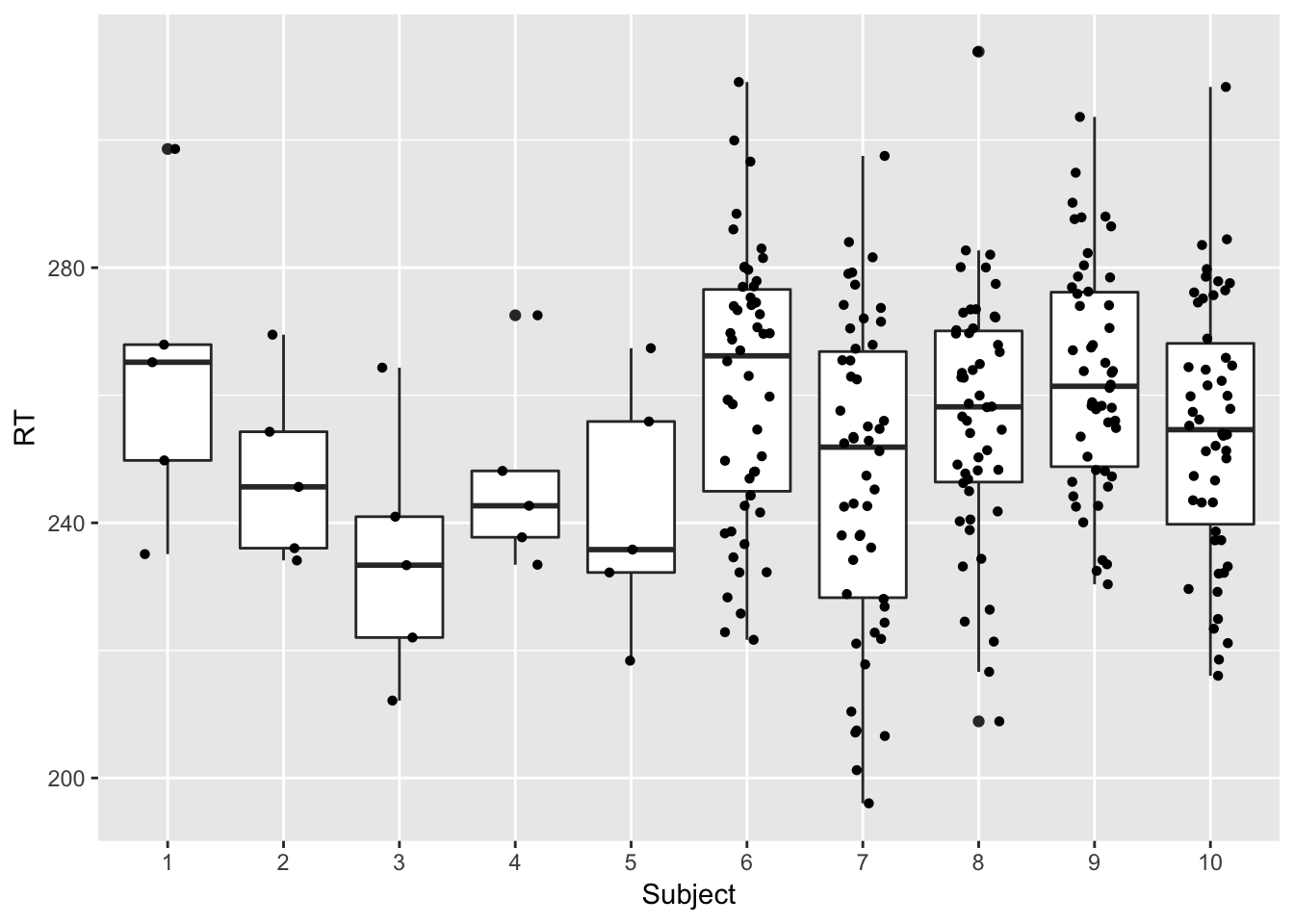
2-stage summary statistics approach compared to conditional modes
Now that the data have been generated, the 2SSS uses a within-subject OLS linear regression model to obtain the within-subject means, \(\hat\beta_i^{OLS}\) and then these are averaged in a second OLS model to obtain the group estimates. The following runs these two stages and also estimates the proper mixed model.
# Stage 1
stage1.est = rep(NA, nsub)
for (i in 1:nsub){
# Estimating the mean RT via OLS
mod.loop = lm(rt ~ 1, dat[dat$subid==i,])
stage1.est[i] = mod.loop$coef[1]
}
#Stage 2
summary(lm(stage1.est ~ 1))##
## Call:
## lm(formula = stage1.est ~ 1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -17.1940 -4.7550 -0.5041 8.5768 11.5654
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 251.754 3.047 82.62 2.82e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.636 on 9 degrees of freedom## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: rt ~ 1 + (1 | subid)
## Data: dat
##
## REML criterion at convergence: 2449.6
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.54753 -0.69671 0.02651 0.72996 2.80661
##
## Random effects:
## Groups Name Variance Std.Dev.
## subid (Intercept) 39.81 6.309
## Residual 423.42 20.577
## Number of obs: 275, groups: subid, 10
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 253.885 2.638 6.206 96.25 4.35e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Comparing the lm summary to the fixed effects summary from the lmer model, the results are almost identical. Although this makes it tempting for many to use 2SSS instead of a mixed model, the next series of videos will set these two modeling approaches apart.
For practice, find the within- and between-subject variance estimates in the lmer summary and compare to the true values used in the simulation.
OLS versus conditional modes
To see the impact of regularization it is necessary to predict the subject-specific values from lmer. As mentioned above, these values are not estimated in any way shape or form during the modeling process above. In the following, the code asks lmer for these predicted values.
The following plot compares the mixed model estimates based on the conditional mean (MMCM, orange) in orange to the within-subject OLS estimates (OLS, blue) from the first stage of the 2SSS. The true mean was….well, the reader should practice understanding the above code by finding that themselves. Once you’ve located that value above, you will notice that the orange dots (MMCM) are shrunken toward the overall group mean compared to the blue OLS estimates. That is a result of the regularization. Recall the first 5 subjects had much less data than the last 5 subjects, which means there’s more likely to be more regularization for the first 5 subjects. I will introduce an equation that describes this exactly in the next chapter, but for now just note the basic trend. It is easiest to see if comparing subject 1 to subject 9. In both cases their within-subject OLS estimates are almost identical, but the MMCM estimate for subject 1 is much smaller! This is reflecting the fact that subject 1 had much less data than subject 9.
subject = rep(c(1:nsub), 2)
estimate = c(mmcm, stage1.est)
estimate.type = rep(c("MMCM", "OLS"), each = nsub)
dat.sub.est = data.frame(subject, estimate, estimate.type)
# Nice colorblind-friendly pallette
# http://www.cookbook-r.com/Graphs/Colors_(ggplot2)/#a-colorblind-friendly-palette
cbPalette <- c("#E69F00", "#56B4E9", "#009E73", "#F0E442", "#0072B2", "#D55E00", "#CC79A7","#999999")
ggplot(dat.sub.est, aes(x = subject, y = estimate,
color = estimate.type)) +
geom_point()+ scale_colour_manual(values=cbPalette) + xlab("Subject")+ylab("RT") + labs(color = "Estimate Type") +
scale_x_continuous(breaks = seq(0 , 10, 1), minor_breaks=seq(0, 10,1))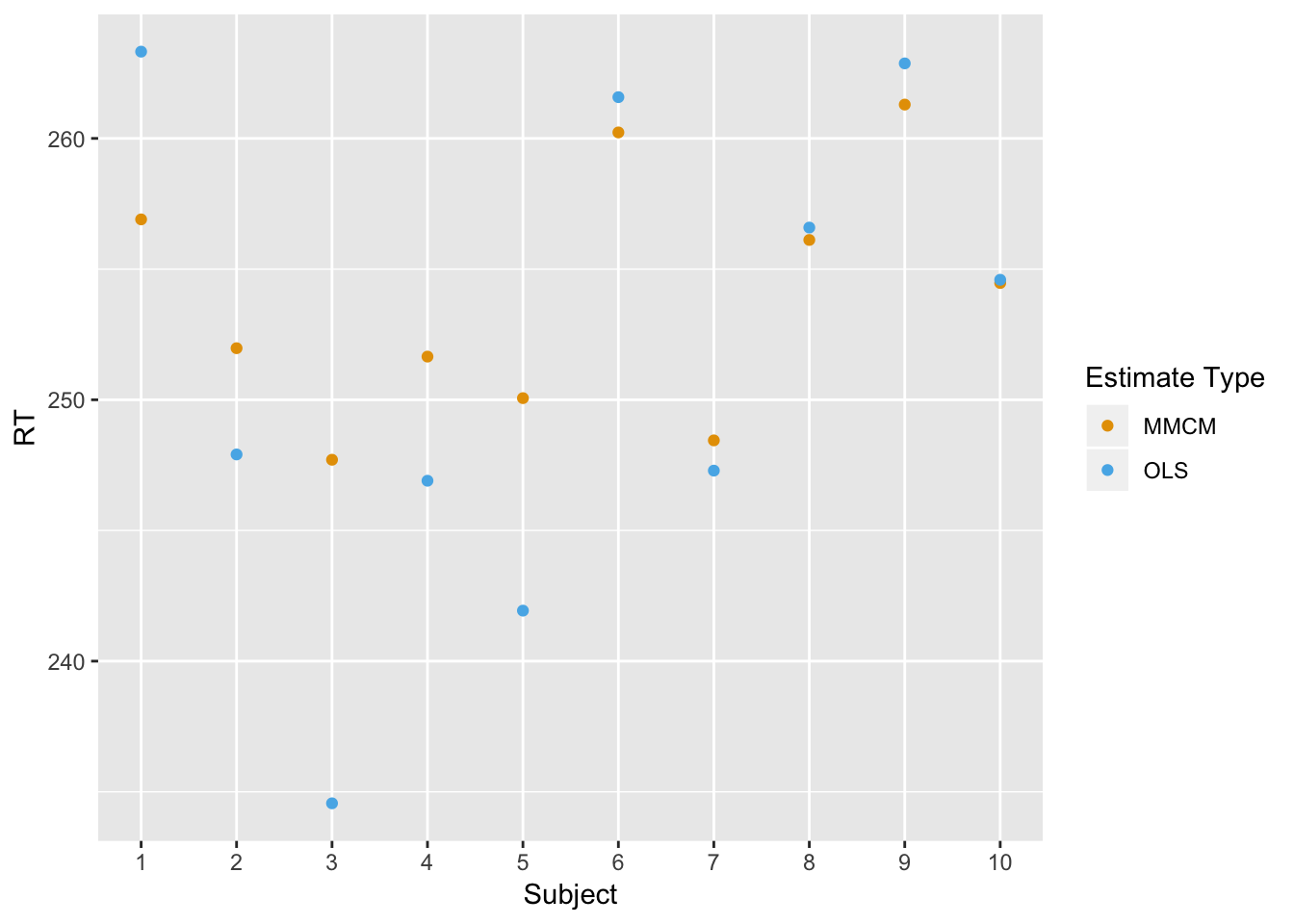
Summary
This document is just a taste of what is to come. This is just a beginning to convince folks analyzing data that data analysis can be done better without using the two-stage summary statistics model, so don’t be tempted! There are cases where you will not have a choice, but generally you will be better off with a mixed model. Future chapters will help clarify when these two approaches will yield similar results.
Although not a perfect way to view the phenomenon, conditional mode-based within-subject estimates from mixed models help in understanding the regularization that happens in the mixed model framework. On the surface it can be thought of as trying to stabilize the estimate from subjects with less data. The important take away for now is that this is driven by the amount of data within-subject.
What inspired this series is that when I explained this point to my colleague she immediately wanted to know how this regularization might impact her between-subject analyses. For example, what if in the fake data above the first 5 subjects were patients and the last 5 were controls. It is a reasonable scenario that some patients may have less data than controls, which is definitely the case for my colleague’s data. If the patients’ estimates are shrunken toward the overall mean because they have less data, could that introduce false positives or reduce power? A really great question! That is what the focus will be in the following chapters where I will use simulated data to compared different modeling approaches. It will also reveal the misleading nature of these conditional mode estimates.